Maximalizace zisku

Zadání úkolu:

Výpočtem hledejte maximální zisk pomocí dvou metod:

1. MC = MR (ekonomické pravidlo)
2. Hledání extrému funkce (využití diferenciálního počtu)

a hledejte spojitosti obou výpočtů.

Zakreslete pod sebe 3 související grafy a do nich VŠECHNY RELEVANTNÍ ÚDAJE A SOUVISLOSTI (POPIŠTE CO NEJVÍCE):

1. TR, TC
2. MR, MC
3. zisk π

Hledejte pro funkce:

• TR = 11 300 Q - 22Q²
• TC = 4 Q³ - 16 Q² + 140 Q + 178

MC = MR, tedy mezní náklady se rovnají meznímu příjmu. My mezní náklady ani příjem neznáme, můžeme si je však odvodit, protože víme, že mezní veličina je derivací veličiny celkové:

TC = 4 Q³ - 16 Q² + 140 Q + 178     =>     MC = 12 Q² - 32 Q + 140

TR =  11 300 Q - 22Q²                             =>     MR = - 44Q + 11 300

Pokud porovnáme získané veličiny, zjistíme, že maximálního zisku dosáhneme při množství Q = 30ks.

Jiným přístupem může být π = TR - TC, kdy dosazením do rovnice získáme:

π = - 4 Q³ - 6 Q² + 11 160 Q - 1780

Získanou funkci zderivujeme, čímž získáváme:

π' = - 12 Q² - 12 Q + 11 160 

Rovnici položíme rovno nule a zjistíme, že Q₁ = 30, Q₂ = -31.

Provedeme druhou derivaci, čímž získáváme:

π'' = - 24 Q + 12 

Po dosazení -31 a 30 získáváme lokální maximum a minimum v bodech -732, resp. 732.

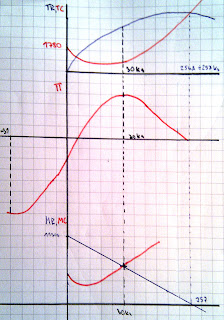
Obrázek č.1: promítnutí funkcí TR, TC a jejich derivací (mezních funkcí) a π v jednom grafu

Veškeré další výpočty pak představují mechanické dosazování hodnot do jednotlivých funkcí. Pro zopakování si uvedeme několik důležitých poznatků:

1. Rovnováha je v bodě, kde MR = MC, tedy mezní náklady se rovnají mezním příjmům.
2. Zisk je v tomto bodě maximální a je roven TR - TC, tedy celkovým příjmům zmenšeným o celkové výdaje.
3. V bodě, kde se mezní náklady rovnají nule, jsou celkové celkové příjmy maximální - zde již z dodatečné jednotky nemáme žádný další příjem.
4. Při výpočtech často narazíme na zápornou hodnotu Q, která je pro ekonomickou realitu nepoužitelná (nenabízíme -31 ks produktu).