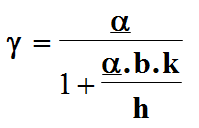Dynamické modelování

Známe rovnice poptávky a nabídky:

Q(d) = 100 - 5P

Q(s)= -20 + 4P

Na základě sklonu křivek zjistíme, že nabídka je zpožděná za poptávkou (má menší sklon).

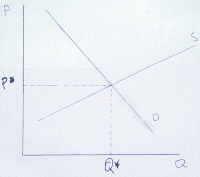
Zakreslením do grafu získáváme Obrázek č. 1:

Obrázek č. 1: nabídka a poptávka

Rovnovážnou cenu P* a množství Q* vypočteme porovnáním obou předpisů:

Q(s) = Q(d)

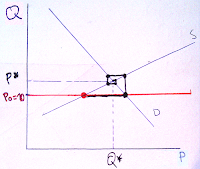
Získáme tak hodnoty P = 13,3 a Q = 33,3. V příkladech bývá zadána výchozí cena -> pro naše demonstrativní účely ji stanovme jako P0 = 10:

Obrázek č. 2: graf s vyznačenou počáteční cenou

Když už známe počáteční cenu a máme zakresleny křivky S a D, můžeme vytvořit tzv. "pavučinový model". V něm je zachycena cena a množství, které se v realitě nachází na trhu, než systém nabude celkově rovnovážného bodu:

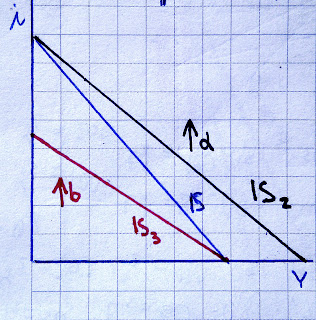
Obrázek č. 3: pavučinový model vývoje cen a množství. POZOR: musel jsem kvůli decentní chybě prohodit osy, v původní konstelaci by šla spirála nejprve nahoru.

Na Obrázku č. 3 zobrazuje černá čára postupnou změnu kvantity a ceny zboží. 

1. V první, nejdelší horizontální části se vychází z počáteční ceny, kdy počítáme s tím, že výrobce je níže, než je globální rovnovážná cena. Výrobce tím pádem vyrábí příliš malé množství a je mu to dáváno najevo nespokojenými kupujícími - v regálech chybí výrobky.
2. Výrobce zvýší cenu a snaží se vyrábět větší množství.
3. Poptávka však cenu tlačí opět dolů, nikomu se nechce konzumovat nadbytek.
4. Výrobci stlačí dolů množství, protože nechtějí vyrábět nadprodukci.

Z modelu krásně vyplývá, jak jsou všechny naše ekonomické modely nepřesné, neboť ve většině příkladů počítáme rovnováhu rovnováhu rovnováhu, ale nikde neřešíme, jak jsme k ni došli. 

Nyní musíme odvodit rovnici dynamické rovnováhy; pokud je nabídka zpožděna o jedno období za poptávkou, budou rovnice vypadat takto:

Q(s t+1) = 100 - 5P(t)

Q(d t+1) = -20 + 4P(t+1)

Položením strany nabídky a poptávky do rovnosti získáme vztah:

4P(t+1) + 5P(t) = 120

Což je hledaná rovnice dynamické rovnováhy. Dále můžeme zjistit tzv. zkrácenou rovnici:

4P(t+1) + 5P(t) = 0

Z ní zjistíme tzv. charakteristickou rovnici a z ní koeficient λ:

4 λ (1) + 5 λ (0) = 0

λ = -5/4

Teorie užitku - funkce dvou proměnných v ekonomii

Máme-li ukázat využití funkce dvou proměnných ve funkci užitku, musíme nejprve vymezit, kam sahá zadání většiny příkladů.


Indiferenční křivky
Jedná se o křivky, které spojují body, v nichž má konzument ze dvou výrobků stejný užitek.

Linie rozpočtu
Čára, která nám udává, co si konzument může dovolit, tedy kam jej pustí jeho rozpočet.

Důchodově spotřební křivka

Obrázek č. 1: Důchodově spotřební křivka

Na obrázku 1 je zachycena situace, kdy se spotřebitel rozhoduje mezi výrobky X a Y na základě toho, jaký má z daných kombinací užitek a co si může dovolit. 

To první - užitek - zachycují jeho indiferenční křivky, paraboly černou barvou.

To druhé - finanční limit - zachycují modré křivky, tzv. isokosty.

Bod optima je tam, kde spotřebitelova rozpočtová linie protíná některou indiferenční křivku.

Když se spotřebitelovi zvedne plat, může si dovolit utratit více peněz, izokosta se tedy posouvá směrem doprava. To způsobí, že spotřebitel dosáhne na svou vyšší indiferenční křivku a najde nové optimum (ve vyšší poloze, tedy kombinace většího množství výrobků X a Y).

Je tedy patrné, že důchodově spotřební křivka (income consume [consumption] curve - ICC) zachycuje vztah spotřebitele k ceně výrobku, za předpokladu, že se bude měnit linie rozpočtu spotřebitele.

Cenově spotřební křivka

Narozdíl od ICC zachycuje PCC (price) situaci, kdy se spotřebitel taktéž rozhoduje mezi dvěma statky, avšak nemění se jeho linie rozpočtu, ale cena jednoho ze dvou statků (kdyby se měnila cena obou statků stejným tempem, jsme opět na ICC).

V praxi nám tak nevzniká posun, ale změna sklonu izokosty.

Extrémní účinky fiskální a monetární politiky

Zadání úkolu:
Vypracujte si přehled extrémních účinků politik. 


Úkol spočívá v analýze extrémních účinků fiskální a monetární politiky, tedy v případech, kdy je křivka IS, resp. LM horizontálně nebo vertikálně položena.


Fiskální expanze:

Obrázek č. 1 - extrémní účinky fiskální politiky

Maximální účinky fiskální politiky nastávají, když se h blíží nekonečnu, resp. b blíží nule. Křivka LM je pak horizontálně položena a v druhém případě je křivka IS zcela vertikální. 

V obou těchto případech je velikost vytěsnění nulová a produkt:

ΔY = γ . ΔA                α = γ 

 Obrázek č. 2 - fiskální multiplikátor

Minimální účinky nastávají při h blížícím se nule nebo b blížícímu se nekonečnu. Křivka LM je pak vertikální, resp. křivka IS horizontální. V obou případě nastává největší možné vytěsnění,

Monetární expanze:

Obrázek č. 3 - extrémní účinky monetární expanze

U monetární expanze je situace podobná, jediným rozdílem je, že nemění sklon, resp. polohu křivky IS, ale měníme sklon, resp. polohu křivky LM.

Obrázek č. 4 - monetární multiplikátor

Maximální změna produktu, v případě maximálního účinku monetární politiky a tedy nulového vytěsnění:

Monetární a fiskální politika

Zadání úkolu:
Modelujte velikost produkce vytěsněné fiskální, resp. monetární politikou.

Trocha teorie zde.
Teorie ve zkratce: vláda může ovlivňovat ekonomiku pomocí tzv. fiskální (rozpočtové) politiky, zatímco centrální banka může ekonomiku ovlivňovat pomocí tzv. monetární (měnové) politiky. V praxi to v ekonomické matematice znamená, že hovoříme-li o fiskální politice, hýbeme s křivkou IS, tedy křivkou rovnováhy na trhu zboží a služeb, na níž mají vliv vládní výdaje, transferové platby a daně, kdežto bavíme-li se o měnové politice, zabýváme se křivkou LM, tedy křivkou rovnováhy na trhu peněz, křivkou, na níž má největší vliv centrální banka.

Mějme zadány hodnoty a z nich vyvozené předpisy křivek:
t=0,25, c=0,8, A0=1000, b=30, k=0,4, M/P = 300

IS: Y = 2,5 * (1000 - 30*i)

LM: i = 0,4*Y - 300

Můžeme pokračovat metodou zjištění souřadnic rovnovážných bodů E0, E1 a Em, kdy E0 získáme vypočtením soustavy rovnic o dvou neznámých:

Eo:    io = 9,5    Yo = 1780     Eo = [9,5 ; 1780]

Předpokládejme, že vláda formou fiskální politiky navýší vládní výdaje nebo transfery o 200 jednotek. Nová rovnováha tedy vyplyne ze stejného výpočtu při změně předpisu křivky IS:

IS': Y = 2,5 * (1200 - 30*i)

LM: i = 0,4*Y - 300

E1:     i1 = 11,5      Y1 = 2137      E1 = [11,5 ; 2657]

Zde však počítáme s rovnováhou, která nastává i při zvýšení úrokové míry. Rozdíl mezi touto rovnováhou a rovnováhou na nové křivce IS pro původní úrokovou míru se nazývá vytěsněná produkce. Poslední zmíněnou rovnováhu získáme dosazením původní i do nové IS:

IS': Y = 2,5 * (1200 - 30*i)

E2:      i2(0) = 9,5       Y2 = 2278     E2 = [9,5 ; 2278]

Obrázek č. 1: grafické znázornění případu fiskální expanze

Konkrétní příklad změny IS-LM

Zadání úkolu:

1. Analytické odvození křivek s různými sklony
2. Grafické odvození křivek s různými sklony
3. Analytické vyjádření křivek s použitím vzorců
4. Grafické zakreslení výsledků

Na následujícím příkladě si ukážeme, jak se konkrétně může měnit přímka LM.

Vycházejme z předpisu L:

L=k*Y - h*i

Budeme měnit K, tedy citlivost poptávky po penězích na změnu úrokové míry, a to z 0.4 na 0.8.

Předpokládejme h=0.5, k=0.4 a k'=0.8, Y1=100, Y2=200.

Dostáváme tedy 4 varianty přímky LM:

L1 = 40 - 0,5*i

L2 = 80 - 0,5*i

L1' = 80 - 0,5*i

L2' = 160 - 0,5*i

Graficky vyjádříme přímky po získání jejich průsečíků s osami souřadnic. Dosazením 0 za jednotlivá L získáme hodnoty i, kterými doplníme informace o bodech rovnováhy na jednotlivých přímkách LM.

E1 = [100 ; 80]

E2 = [200 ; 160]

E1' = [100 ; 160]

E2' = [200 ; 320]

Obrázek č. 1: Grafické znázornění změny sklolu LM vlivem změny k.

Jak vidíme, na příkladu jsme v podstatě ověřili správnost závěrů minulého úkolu, tedy že se změnou k se mění sklon přímky LM, máme-li tedy koeficient k menší, resp. větší, je LM plošší, resp. strmější.

Sklony a posuny křivek IS, LM

Zadání úkolu:
Které veličiny ovlivní sklon, resp. posun křivky IS, resp. LM? 

Nejprve trocha teorie z wikipedie pro usnadnění pochopení.

Předpis křivky IS je dán rovnicí:

IS: Y =  α  . (A - b*i)

Kde Y je důchod, α je výdajový multiplikátor, A jsou autonomní výdaje, b je citlivost investic na změnu úrokové míry a i je úroková míra.

Předpis křivky LM je dán rovnicí:

LM:

Kde k je citlivost poptávky po penězích na změnu důchodu, h  je citlivost poptávky po penězích na změnu úrokové míry a M/P je nabídka peněz, kterou určuje centrální banka.

Obrázek č. 1: sklon křivky IS

Obrázek č. 1 zachycuje změnu sklonu přímky IS. Taková situace může nastat, pokud se mění výdajový multiplikátor (černá přímka IS2) nebo pokud se mění citlivost investic na změnu úrokové míry (červená přímka IS1).

Obrázek č. 2: posun křivky IS

Obrázek č. 2 zachycuje posun přímky IS, který nastane buď navýšením (červená přímka IS3) nebo snížením (černá přímka IS2) autonomních výdajů.

Obrázek č. 3: změna sklonu přímky LM

Přímka LM může svůj sklon změnit, když se změní koeficienty k nebo h. Tzn., jak ukazuje obrázek č. 3, stoupne-li citlivost poptávky po penězích na důchod nebo stoupne-li citlivost poptávky po penězích, je přímka LM strmější (jako černá LM2) a naopak (jako červená LM3).

Obrázek č.4: posun přímky LM

Pokud se mění nabídka peněz, posouvá se celá přímka LM, a to buď doprava nebo doleva (pokud M/P roste, resp. klesá).

Akumulace kapitálu

Ihned na počátku této kapitoly je dobré vysvětlit si pojmy toková a stavová veličina. Toková veličina vyjadřuje velikost něčeho měřenou např. v určitém časovém období, zatímco veličina stavová zachycuje okamžitý stav.
Nyní můžeme pochopit rozdíl mezi kapitálovým tokem a hodnotou kapitálu.


Kapitálový tok je funkcí kapitálu v čase: K(t)=t^2 +1.
Hodnota kapitálu pak vyjadřuje hodnotu této funkce v daném okamžiku: K(2)=2^2 + 1 = 5.

Vztah mezi kapitálovým a investičním tokem
Investice se dají chápat jako tok výdajů, kterým můžeme navýšit hodnotu kapitálu. Investiční tok vyjadřuje změnu kapitálu v určitém období.

I(t) = ΔK / Δt

V praxi známe pouze funkci investičního toku, abychom získali funkci kapitálového toku, musíme funkci investičního toku derivovat, a naopak, chceme-li z funkce kapitálového toku zjistit funkci investičního toku, musíme funkci kapitálového toku integrovat.

K(t) = I(t)'

I(t) = K(t)

Vztah mezi hodnotou akumulovaného kapitálu vyjádřenou investiční funkcí a kapitálovou funkcí je vysvětlen na Obrázku č.1. Zakreslujeme-li do grafu kapitálovou funkci, pak hodnota akumulovaného kapitálu představuje vzdálenost na ose závisle proměnné v daném časovém úseku (čas zde bereme jako nezávisle proměnnou). Naopak, zakreslujeme-li do grafu investiční funkci, velikost akumulovaného kapitálu představuje plocha mezi dvěma časy a křivkou investiční funkce.

Obrázek č.1: investiční a kapitálová funkce a vyjádření hodnoty akumulovaného kapitálu (u kapitálové funkce se jedná o červený úsek na vertikální ose.

Jednoduchou úvahou zjišťujeme, že ke konkrétní hodnotě dorazíme buď pomocí určitého integrálu a dvou hodnot času při použití investiční funkce nebo rozdílem dvou funkčních hodnot pro dva časy při použití funkce kapitálové. Oběma postupy docházíme ke stejnému výsledku.